Milui hat geschrieben:Ein Fixed-Effects Modell scheidet meiner Meinung nach aus, weil mich 1) zeitkonstante Merkmale interessieren (die soziale Integration, Geschlecht) und diese im FE-Modell zwar berücksichtigt, aber nicht geschätzt werden können und 2) weil die zentrale AV die Veränderung der Gesundheit zwischen zwei Zeitpunkten ist.
1) kann ich (teilweise) nachvollziehen. Man könnte einwenden, dass zeitkonstante Faktoren keinen kausalen Effekt (im Sinne des kontrafaktischen Modells) haben können, aber das ist eine andere Diskussion. Schwerwiegender ist das Problem unbeobachteter Heterogenität, das Du selbst ansprichst. Bei 2) verstehe ich gar nicht was gegen ein FE Modell spricht, aber das ist auch nebensächlich.
Wenn ich die Gesundheit in 2001 vor dem Ereignis betrachte und dann 2006 nach dem Ereignis, dann ist das ein Vergleich zwischen zwei Perioden und für so etwas müsste eine pooled Regression (mit robusten Standardfehlern bzw. vce(cluster) Option in Stata) ausreichen,oder?
Ja, wenn Du davon ausgehst, dass es keine unbeobachtete Heterogenität gibt, oder Du diese vollständig modellieren kannst.
Ich könnte vielleicht ein Random-Effects-Modell rechnen, um die zeitkonstanten Merkmale zu schätzen. Diese Schätzer sind bei unbeobachteter Heterogenität verzerrt.
Genau wie im pooled Model (s.o.). Der Vorteil des RE gegenüber dem pooled Model ist Effizienz in ersterem (bei korrekter Modelspezifikation!).
[...] aber es wird trotzdem unbeobachtete Heterognität vorliegen...
Wenn das der Fall ist, dann kannst Du weder RE noch pooled konsistent schätzen (s.o.). FE (oder FD) Modelle sind die einzige Möglichkeit mit (zeitkonstanter!) unbeobahteter Heterogenität umzugehen.
Aber zurück zur Frage: gibt es denn keinen einfachen Weg, die Veränderung in der Gesundheit zu modellieren?
M.E. gibt es keine
einfache Möglichkeit. Das mag an meinem begrenzten Verständnis liegen, aber ich bilde mir ein, dass dies nicht der Fall ist.
Eine Möglichkeit ist die Spezifikation eines Modells mit der Gesundeheit 2006 als outcome und der Gesundheit 2000 als zusätzlichem Prädikator. Die intuitive Idee dahinter ist, dass alles was die Gesundheit 2000 beeinflusst bereits in dem Geschätzen Koeffizienten "abgefangen" ist und die Koeffizienten für die übrigen Prädikatoren dann den Effekt dieser Prädikatoren auf die Entwicklung der Gesundheit abbilden. Das geht in Richtung growth curve Modelle. Ich bin aber alles andere als sicher, dass das eine gute Idee ist. Ich skizziere kurz mein Problem mit diesen Modellen (siehe auch Halaby 2004)
Nimm an Du spezifizierst
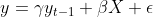
mit
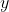
Gesundheit 2006,
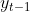
Gesundheit 2000,
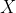
zeitkonstante Prädikatoren.
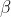
und
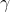
sind zu schätzende Parameter, die dann konsistent geschätzt werden, wenn
 = 0)
.
Teilen wir

in zeitkonstante unbeobachtete Heterogenität
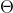
und (unbeobachtete) Heterogenität, die über Zeit variiert
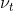
und schrieben wir das Modell als
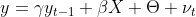
Hier wird deutlich, dass unsere Annhame schon durch die Modelformulierung verletzt ist. Da
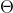
zeitkonstant ist und
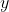
beeinflusst, beeinflusst es auch
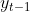
.
Ähnliche Probleme kann ich mir vorstellen, wenn Du einfach eine Differenz der beiden Gesundheitswerte berechnest und diese dann als outcome in einem Modell verwendest. Beide Modell findest in häufig in der Literatur, das ändert aber nichts an den Problemen, die offensichtlich selten bedacht werden.
Mich interessiert wie sich die Gesundheit der Personen durch das Erleben verschiedener Ereignisse (sagen wir bspw. Heirat) verändert. Insbesondere soll der Effekt sozialer Integration auf diesen Zusammenhang geklärt werden (Direkteffekt + Puffereffekt).
Das solltest Du mal noch genauer ausführen. Ich habe keine Ahnung was ein "Puffereffekt" ist, aber die Formulieriung klingt nach einer Interaktion (i.e. einer multiplikativen Verknüpfung) zwischen Heirat und sozialer Intergration auf Gesundheit. Du kannst in FE Modellen zwar keine zeitkonstanten Effekte schätzen, sehr wohl aber Interaktionen von zeitinvariaten mit zeitveränderlichen Faktoren.
Mir scheint hier geht es tatsächlich weniger um Stata syntax, daher würde ich ersthaft überlegen, diese Diskussion im Statisitkforum fortzusetzen. Mir scheint da sind mehr Leute aktiv als hier, was die Chance auf eine produktive Diskussion steigert.
Halaby, Charles N. (2004). Panelmodels in Sociological Research: Theory into Practice. Annu. Rev. Sociol. 30:507–44.
Stata is an invented word, not an acronym, and should not appear with all letters capitalized: please write “Stata”, not “STATA”.